Vector equation & Cartesian equation of a line

Vector equation

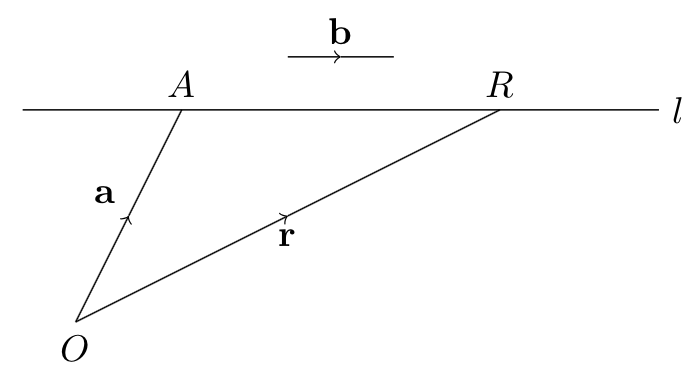
The vector equation of line $l$ is given by $$ \boxed{ l : \textbf{r} = \textbf{a} + \lambda \textbf{b}, \lambda \in \mathbb{R} } $$

$\textbf{r}$ is the position vector of a point on line $l$ (i.e. $\overrightarrow{OR}$)

$\textbf{a}$ is the position vector of a known point on line $l$ (i.e. $\overrightarrow{OA}$)

$\textbf{b}$ is the direction vector which is parallel to line $l$

Cartesian equation

General form: $$ \boxed{ {x - a_1 \over b_1} = {y - a_2 \over b_2} = {z - a_3 \over b_3} } $$

Convert from one form to the other

\begin{align} l : \textbf{r} & = \left( \begin{matrix} 1 \\ 2 \\ 3 \end{matrix} \right) + \lambda \left( \begin{matrix} 3 \\ 2 \\ 1 \end{matrix} \right), \lambda \in \mathbb{R} \\ \\ \text{Let } & \textbf{r} = \left( \begin{matrix} x \\ y \\ z \end{matrix} \right), \\ \\ \left( \begin{matrix} x \\ y \\ z \end{matrix} \right) & = \left( \begin{matrix} 1 + 3\lambda \\ 2 + 2\lambda \\ 3 + \lambda \end{matrix} \right) \\ \\ x & = 1 + 3 \lambda \implies \lambda = {x - 1 \over 3} \\ y & = 2 + 2 \lambda \implies \lambda = {y - 2 \over 2} \\ z & = 3 + \lambda \implies \lambda = z - 3 \\ \\ \text{Cartesian equation: } & \phantom{0} {x - 1 \over 3} = {y - 2 \over 2} = z - 3 \end{align}

\begin{align} \text{Cartesian equation: } & {1 - x \over 2} = z + 2, \phantom{0} y = 0 \\ \\ \mu & = {1 - x \over 2} \implies x = 1 - 2\mu \\ \mu & = z + 2 \implies z = -2 + \mu \\ & \phantom{000000000000.} y = 0 \\ \\ \left( \begin{matrix} x \\ y \\ z \end{matrix} \right) & = \left( \begin{matrix} 1 - 2\mu \\ 0 \\ -2 + \mu \end{matrix} \right) \\ \\ l : \textbf{r} = \left( \begin{matrix} 1 \\ 0 \\ -2 \end{matrix} \right) & \phantom{.} + \mu \left( \begin{matrix} -2 \\ 0 \\ 1 \end{matrix} \right), \mu \in \mathbb{R} \end{align}