Inverse function: Rule, Domain, Rule & Graph

Example

$$g : x \mapsto x^2 - 2x - 2, \phantom{000} x \in \mathbb{R}, 1 \le x \le 4$$

$g$ is a 1-1 function and $$D_g = [1, 4], R_g = [-3, 6]$$

Domain & Range

The domain and range of $f$ and its inverse $f^{-1}$ are related by: $$\boxed{ D_f = R_{f^{-1}} }$$ $$\boxed{ R_f = D_{f^{-1}} }$$

Example

$$g : x \mapsto x^2 - 2x - 2, \phantom{000} x \in \mathbb{R}, 1 \le x \le 4$$

and $$D_g = [1, 4] \text{ and } R_g = [-3, 6]$$

Since the inverse function ‘reverses’ the original function, $$D_{g^{-1}} = R_g = [-3, 6]$$ $$R_{g^{-1}} = D_g = [1, 4]$$

Rule of inverse function

Example

$$g : x \mapsto x^2 - 2x - 2, \phantom{000} x \in \mathbb{R}, 1 \le x \le 4$$

Step 1: Let y = g(x): $$y = x^2 - 2x - 2$$

Step 2: Make x the subject and reject the inappropriate expression given $D_g = [1 , 4]$ $$\begin{align} y + 2 & = x^2 - 2x \\ y + 2 & = \left(x - {2 \over 2}\right)^2 - \left(2 \over 2\right)^2 \\ y + 2 & = (x - 1)^2 - (1)^2 \\ y + 2 & = (x - 1)^2 - 1 \\ y + 3 & = (x - 1)^2 \\ \pm \sqrt{y + 3} & = x - 1 \\ 1 \pm \sqrt{y + 3} & = x \\ \\ \text{Since } & D_f = [1, 4], \\ x & = 1 + \sqrt{y + 3} \end{align}$$

Step 3: Form g^-1 by replacing y with x $$g^{-1} : x \mapsto 1 + \sqrt{x + 3}, \phantom{000} x \in \mathbb{R}, -3 \le x \le 6$$

Graph of inverse function

Example

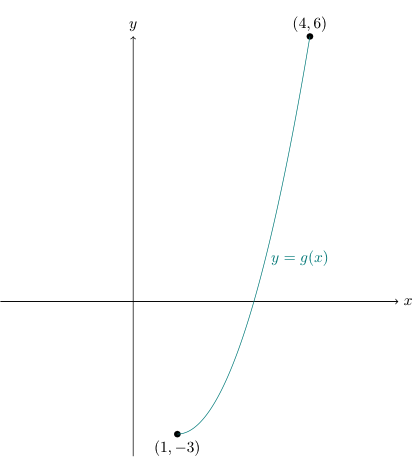
Given $$g : x \mapsto x^2 - 2x - 2, \phantom{000} x \in \mathbb{R}, 1 \le x \le 4$$

and $$D_g = [1, 4] \text{ and } R_g = [-3, 6]$$